High latency between miners gives an exponential advantage to miners closer to the highest concentration of compute. Unless this problem is solved, it is not possible to mine Bitcoin on multiple planets at the same time. Mining "collapses" to the single largest low-latency mining cluster.
Consider the following thought experiment.
There are exactly 2 computers in the universe, sitting 60 light minutes away from each other. Each is exactly as powerful as the other, and both are spending all of their compute mining bitcoin. Suppose they both start mining the same block at the same time ("same time" according to an observer sitting halfway between them). After about 10 minutes, one of them (call it computer A) will have mined the first block. A sends it over to B.
But it takes 60 minutes for the block to arrive at computer B. In that time, B will have mined an expected 3 blocks. A's block is 2 blocks behind, so B will ignore it. Furthermore, this effect is symmetric: locally, each computer has a 60-minute lead, and remotely, each one has a 60-minute penalty. In order to agree on a block, one of the computers would have to get lucky enough that its chain is longer even with the 60-minute penalty.
We can run a Monte Carlo simulation to see what percentage of blocks accepted by both machines were generated by A.[1]
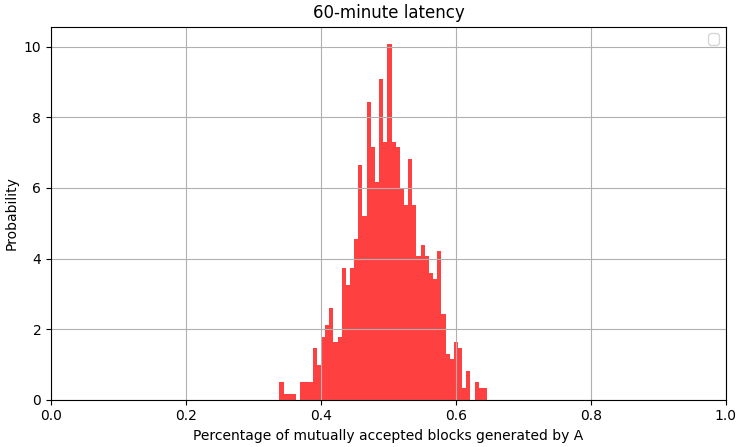
This looks like what we expect. Computer A is expected to mine 50% of the blocks. What happens when we change the percentage of compute that A has?
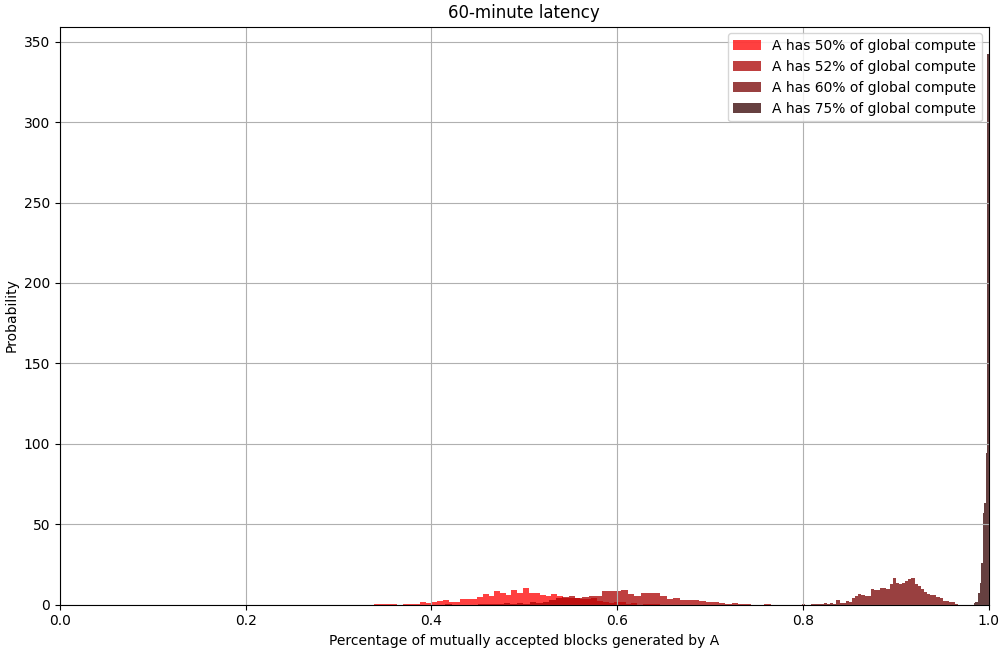
Uh-oh. When A has 75% of the compute, it mines an expected 99.8% of mutually accepted blocks. B spends more than 1000 times the compute per accepted block![2]
As B's percentage of global compute falls, it's likelihood of overcoming the latency falls exponentially. It has to get increasingly more lucky in order to get a long enough streak of blocks.[3]
60 minutes of latency is slightly farther than the maximum distance between Earth and Jupiter. What if we just want to mine Bitcoin on Earth and Mars – an average of 12 light minutes apart?
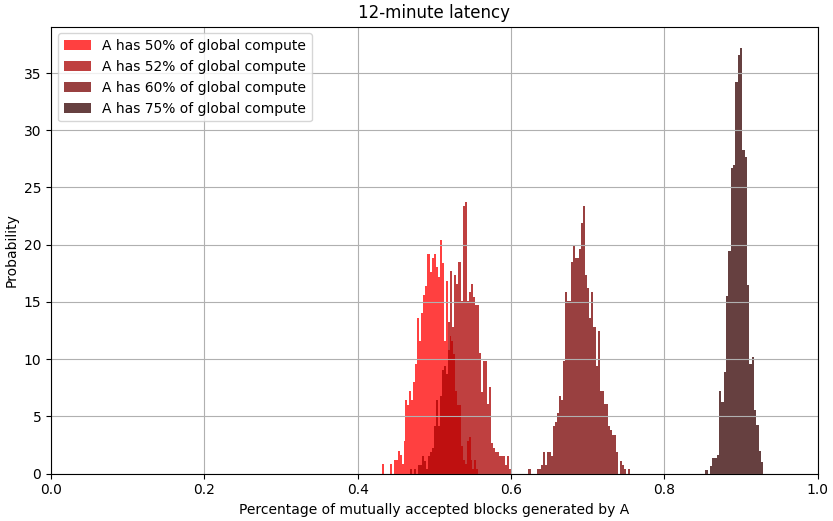
This is a lot better than the 60-minute scenario, but B is still spending 3x as much compute for every accepted block.[4] Unless B has access to abundant, very cheap compute, it would not make sense for it to continue mining. But if B has access to such a resource, it can likely mine harder than A can, in which case the effect is reversed – it doesn't make sense for A to continue mining.
The location with the highest concentration of compute has an exponential advantage in mining blocks, and ends up being the de facto "bitcoin emitter". It will be nearly a pure loss to mine anywhere except the epicenter of compute, so every other location would stop mining, giving the epicenter a complete monopoly on producing blocks.
It seems like this effect may cause Bitcoin to devolve into a fiat currency. If Earth is where all the bitcoin is mined, the miners on Earth have incentive to collude for the benefit of Earth, and they cannot be stopped since no other planet can mine. What prevents terrestrial miners from imposing a minimum transaction fee on all addresses known to be Martian? Why would Earth not impose sanctions on Martian addresses when Martian policies negatively affect Earth? Bitcoin's security relies on the inability to concentrate compute, but high latency forces its concentration.
Furthermore, every transaction needs to make a round trip to the epicenter, so confirmation times would scale linearly with the distance between where the transaction originated and the center.
One way to fix this, is for everyone to agree to increase the difficulty so that latency is always negligible compared to the time to mine a block. This avoids the monopoly on mining, but now the confirmation time of every single transaction grows linearly with the maximum latency in the network! This doesn't seem like a viable solution – the latency between miners on Earth and Mars is 1000x higher than between miners on Earth. It's also not clear why those near the epicenter would even agree to such a change – it makes the protocol strictly worse for them.
The Lightning Network could be used to somewhat mitigate the confirmation time problem. It would allow local transactions to be done at real-time speeds, once a channel is opened. But each channel still requires two on-chain transactions in order to open/close.
This seems like a vital problem for Bitcoin to solve, if we want it to survive for at least another 50 years. Did I make an error in my calculations? If not, does anybody have ideas for solutions? Please reach out on twitter.
Notes
[1]: I ran 1000 simulations of mining 2000 mutually accepted blocks at a fixed difficulty. Each vertical bar in the histogram shows how many of the simulations ended up with A mining the given percentage of mutually accepted blocks.
[2]: A spends 75% of global compute on 99.8% of the blocks. B spends 25% of global compute on 0.02% of the blocks. B spends 1,663 times as much compute per block.
[3]: Suppose B has 25% of global compute. If there is 0 latency, B just has to get one block ahead of A in order to be accepted. That happens 25% of the time. If there are 60 minutes of latency, B has to get 4 blocks ahead of A in order to be accepted. That happens 0.254 = 0.003% of the time.
[4]: A spends 75% of global compute on 90% of the blocks. B spends 25% of global compute on 10% of the blocks. B spends 3 times as much compute per block. It's important to note that difficulty was not adjusted in the simulation. Under high latency, many mined blocks are discarded, so difficulty gets adjusted lower. A lower difficulty exacerbates the effect of latency since more blocks are mined and there is less opportunity for low-compute entities to get lucky. A more complete simulation would actually show more extreme results than I've presented here.
